Matemáticas para administración y economía.
Haeussler Jr.
Décimo segunda edición
Matematicas 1
domingo, 24 de mayo de 2015
Resumen
En esta última unidad vimos los temas un poco mas a prisa ya que no había mucho tiempo para explicarse mejor pero fueron temas sencillos y fáciles de entender ademas de que en el salón estuvimos realizando varios ejercicios para aprender mas sobre ellos y el profesor hizo la clase muy dinámica pasando a los alumnos a participar al pizarrón
Bibliografías
unidad 5
http://www.zonaeconomica.com/teoria-utilidad-demanda/elasticidad/ingreso
http://www.eumed.net/cursecon/4/elasticidad-demanda.htm
http://www.sangakoo.com/es/temas/maximizacion-y-minimizacion
http://www.vitutor.com/fun/5/a_4.html
http://es.wikipedia.org/wiki/Punto_de_inflexi%C3%B3n
http://ed21.webcindario.com/CalculoDiferencial/prueba_de_la_segunda_derivada.htm
http://es.wikipedia.org/wiki/Criterio_de_la_primera_derivada
https://sites.google.com/site/virtualcdcasasceduardo/5-aplicacion-de-la-derivada/conceptos-de-extremos-absolutos
http://www.sectormatematica.cl/contenidos/funcreyd.htm
unidad 4
http://es.wikipedia.org/wiki/Diferencial_de_una_funci%C3%B3n
http://dieumsnh.qfb.umich.mx/DIFERENCIAL/derivadas_de_orden_superior.htm
http://www.dervor.com/derivadas/derivacion_logaritmica.html
http://ed21.webcindario.com/CalculoDiferencial/derivacion_implicita.htm
http://www.dervor.com/derivadas/derivada_exponencial.html
http://www.dervor.com/derivadas/derivada_logaritmo.html
unidad 3
http://definicion.de/derivada/
http://es.wikipedia.org/wiki/Diferencial_de_una_funci%C3%B3n
http://definicion.de/razon-de-cambio/
http://www.zweigmedia.com/MundoReal/calctopic1/contanddiffb.html
http://ed21.webcindario.com/CalculoDiferencial/Diferenciabilidad_y_continuidad.htm
http://ed21.webcindario.com
http://es.wikipedia.org/wiki/Regla_de_la_cadena
http://derivadasencalculo.blogspot.mx/p/regla-de-potencias.html
unidad 2
http://es.wikipedia.org/wiki/L%C3%ADmite_matem%C3%A1tico
http://www.vitutor.com/fun/3/a_1.html
http://www.vitutor.com/
http://www.vitutor.com/fun/3/a_2.html
http://www.disfrutalasmatematicas.com/calculo/limites-infinito.html
http://www.vitutor.com/fun/3/b_4.html
unidad 1
http://funcionesespecializacion.blogspot.mx/2010/10/la-notacion-funcional.html
http://artigoo.com/dominio-y-rango-de-una-funcion
http://www.vitutor.com/fun/2/c_1.html
http://www.sectormatematica.cl/contenidos/funoper.htm
http://www.vitutor.com/fun/2/a_4.html
http://es.wikipedia.org/wiki/Gr%C3%A1fica_de_una_funci%C3%B3n
http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/
http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/funciones3/impresos/quincena10.pdf
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Funciones_en_la_Ciencia/oferdem.htm
http://addimate.blogspot.mx/2014/05/funciones-de-apreciacion-y-depreciacion.html
http://www.zonaeconomica.com/teoria-utilidad-demanda/elasticidad/ingreso
http://www.eumed.net/cursecon/4/elasticidad-demanda.htm
http://www.sangakoo.com/es/temas/maximizacion-y-minimizacion
http://www.vitutor.com/fun/5/a_4.html
http://es.wikipedia.org/wiki/Punto_de_inflexi%C3%B3n
http://ed21.webcindario.com/CalculoDiferencial/prueba_de_la_segunda_derivada.htm
http://es.wikipedia.org/wiki/Criterio_de_la_primera_derivada
https://sites.google.com/site/virtualcdcasasceduardo/5-aplicacion-de-la-derivada/conceptos-de-extremos-absolutos
http://www.sectormatematica.cl/contenidos/funcreyd.htm
unidad 4
http://es.wikipedia.org/wiki/Diferencial_de_una_funci%C3%B3n
http://dieumsnh.qfb.umich.mx/DIFERENCIAL/derivadas_de_orden_superior.htm
http://www.dervor.com/derivadas/derivacion_logaritmica.html
http://ed21.webcindario.com/CalculoDiferencial/derivacion_implicita.htm
http://www.dervor.com/derivadas/derivada_exponencial.html
http://www.dervor.com/derivadas/derivada_logaritmo.html
unidad 3
http://definicion.de/derivada/
http://es.wikipedia.org/wiki/Diferencial_de_una_funci%C3%B3n
http://definicion.de/razon-de-cambio/
http://www.zweigmedia.com/MundoReal/calctopic1/contanddiffb.html
http://ed21.webcindario.com/CalculoDiferencial/Diferenciabilidad_y_continuidad.htm
http://ed21.webcindario.com
http://es.wikipedia.org/wiki/Regla_de_la_cadena
http://derivadasencalculo.blogspot.mx/p/regla-de-potencias.html
unidad 2
http://es.wikipedia.org/wiki/L%C3%ADmite_matem%C3%A1tico
http://www.vitutor.com/fun/3/a_1.html
http://www.vitutor.com/
http://www.vitutor.com/fun/3/a_2.html
http://www.disfrutalasmatematicas.com/calculo/limites-infinito.html
http://www.vitutor.com/fun/3/b_4.html
unidad 1
http://funcionesespecializacion.blogspot.mx/2010/10/la-notacion-funcional.html
http://artigoo.com/dominio-y-rango-de-una-funcion
http://www.vitutor.com/fun/2/c_1.html
http://www.sectormatematica.cl/contenidos/funoper.htm
http://www.vitutor.com/fun/2/a_4.html
http://es.wikipedia.org/wiki/Gr%C3%A1fica_de_una_funci%C3%B3n
http://matematicasmodernas.com/funciones-lineales-y-cuadraticas/
http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/funciones3/impresos/quincena10.pdf
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Funciones_en_la_Ciencia/oferdem.htm
http://addimate.blogspot.mx/2014/05/funciones-de-apreciacion-y-depreciacion.html
Elasticidades: elasticidad de la demanda y elasticidad del ingreso.
Elasticidad Ingreso
Al igual que la demanda puede ser medida por un coeficiente como la elasticidad precio de la demanda, ésta puede ser medida pero tomando como variable el ingreso de los consumidores. La ecuación es la siguiente:
ηI=ΔQ/ΔI . I/Q
En esta ecuación se mide la variación porcentual del consumo cuando aumenta el ingreso de los consumidores. Este coeficiente puede ser positivo o negativo. Si es positivo significa que el bien en estudio, el cual varía su consumo, es un bien normal, y si el coeficiente es negativo, el bien será inferior. Este coeficiente se puede estimar teniendo una función de demanda con los coeficientes respectivos, siguiendo los pasos dados en el caso de la elasticidad precio de la demanda.
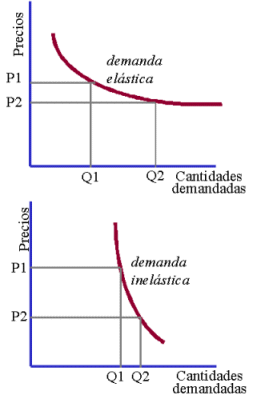
La elasticidad de la demanda
Hay algunos bienes cuya demanda es muy sensible al precio, pequeñas variaciones en su precio provocan grandes variaciones en la cantidad demandada. Se dice de ellos que tienen demanda elástica. Los bienes que, por el contrario, son poco sensibles al precio son los de demanda inelástica o rígida. En éstos pueden producirse grandes variaciones en los precios sin que los consumidores varíen las cantidades que demandan. El caso intermedio se llama de elasticidad unitaria.
La elasticidad de la demanda se mide calculando el porcentaje en que varía la cantidad demandada de un bien cuando su precio varía en un uno por ciento. Si el resultado de la operación es mayor que uno, la demanda de ese bien es elástica; si el resultado está entre cero y uno, su demanda es inelástica.
Los factores que influyen en que la demanda de un bien sea más o menos elástica son:
1) Tipo de necesidades que satisface el bien. Si el bien es de primera necesidad la demanda es inelástica, se adquiere sea cual sea el precio; en cambio si el bien es de lujo la demanda será elástica ya que si el precio aumenta un poco muchos consumidores podrán prescindir de él.
2) Existencia de bienes sustitutivos. Si existen buenos sustitutos la demanda del bien será muy elástica. Por ejemplo, un pequeño aumento en el precio del aceite de oliva puede provocar que un gran número de amas de casa se decida por usar el de girasol.
 |
3) Importancia del bien en términos de coste. Si el gasto en ese bien supone un porcentaje muy pequeño de la renta de los individuos, su demanda será inelástica. Por ejemplo, el lápiz. Las variaciones en su precio influyen muy poco en las decisiones de los consumidores que desean adquirirlos.
4) El paso del tiempo. Para casi todos los bienes, cuanto mayor sea el período de tiempo considerado mayor será la elasticidad de la demanda. Puede ser que al aumentar el precio de la gasolina, su consumo no varíe mucho, pero al pasar el tiempo podrá ser substituida en algunos de sus usos por el carbón, en otros usos por el alcohol, de forma que la disminución en la demanda sólo se nota cuando pasa el tiempo.
5) El precio. finalmente hay que tener en cuenta que la elasticidad de la demanda no es la misma a lo largo de toda la curva. Es posible que para precios altos la demanda sea menos elástica que cuando los precios son más bajos o al revés, dependiendo del producto de que se trate.
Optimización de funciones económico-administrativas: maximización de funciones de ingreso, utilidad y beneficios ;minimización de funciones de costos y costos promedio.
Optimización es el proceso de hallar el máximo o mínimo relativo de una función, generalmente sin la ayuda de gráficos.
En el caso más simple, un problema de optimización consiste en maximizar o minimizar una función real eligiendo sistemáticamente valores de entrada (tomados de un conjunto permitido) y computando el valor de la función. La generalización de la teoría de la optimización y técnicas para otras formulaciones comprende un área grande de las matemáticas aplicadas. De forma general, la optimización incluye el descubrimiento de los "mejores valores" de alguna función objetivo dado un dominio definido, incluyendo una variedad de diferentes tipos de funciones objetivo y diferentes tipos de dominios.
Concavidad, puntos de inflexión y prueba de la segunda derivada.
Concavidad:


Hemos tomado el criterio de que el valle tiene forma convexa y la montaña forma cóncava.
Es posible encontrar textos en los que se define la concavidad y la convexidad de manera opuesta, usando el criterio de que el valle tiene forma cóncava y la montaña forma convexa.
Pero esta definición que damos no sólo alude a un criterio visual que puede ser confuso desde el punto de vista del observador, sino que podemos dar una definición más precisa:
Una función es cóncava en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo x1 y x2, el segmento que une los puntos (x1, f(x1)) y (x2, f(x2)) siempre queda por debajo de la gráfica.

Una función es convexa en un intervalo de su dominio cuando:
Dados dos puntos cualesquiera de dicho intervalo x1 y x2, el segmento que une los puntos (x1, f(x1)) y (x2, f(x2)) siempre queda por encima de la gráfica.

Punto de inflexión
Un punto de inflexión es un punto donde los valores de x de una función continua pasa de un tipo de concavidad a otra. La curva "atraviesa" la tangente. Matemáticamente la derivada segunda de la función f en el punto de inflexión es cero, o no existe.
En el cálculo de varias variables a estos puntos de inflexión se les conoce como puntos de ensilladura.
En las funciones derivables reales de una variable real, para hallar estos puntos de inflexión, basta con igualar la segunda derivada de la función a cero y despejar. Los puntos obtenidos deberán ser sustituidos en la derivada tercera o sucesivas hasta que nos dé un valor diferente de cero. Cuando esto suceda, si la derivada para la que es distinto de cero es impar, se trata de un punto de inflexión; pero, si se trata de derivada par, no lo es. Más concretamente:
- Se halla la primera derivada de
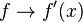
- Se halla la segunda derivada de

- Se halla la tercera derivada de
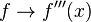
- Se iguala la segunda derivada a 0:
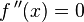
- Se despeja la variable independiente y se obtienen todos los valores posibles de la misma:
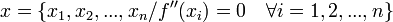 .
. - Se halla la imagen de cada
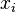 sustituyendo la variable dependiente en la función.
sustituyendo la variable dependiente en la función. - Ahora, en la tercera derivada, se sustituye cada
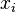 :
:- Si
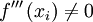 , se tiene un punto de inflexión en
, se tiene un punto de inflexión en 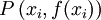 .
. - Si
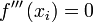 , debemos sustituir
, debemos sustituir 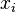 en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que
en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que 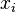 no sea nulo, hay que ver qué derivada es:
no sea nulo, hay que ver qué derivada es:- Si la derivada es impar, se trata de un punto de inflexión.
- Si la derivada es par, no se trata de un punto de inflexión.
- Si
La ecuación 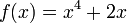 no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en
no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en 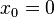 la derivada segunda se anula y la primera derivada no nula en
la derivada segunda se anula y la primera derivada no nula en 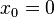 es la derivada cuarta, que es par. Obsérvese que
es la derivada cuarta, que es par. Obsérvese que  tampoco presenta un extremo en
tampoco presenta un extremo en  .
.
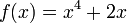 no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en
no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en 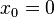 la derivada segunda se anula y la primera derivada no nula en
la derivada segunda se anula y la primera derivada no nula en 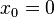 es la derivada cuarta, que es par. Obsérvese que
es la derivada cuarta, que es par. Obsérvese que  tampoco presenta un extremo en
tampoco presenta un extremo en  .
.
Con la prueba de la segunda derivada se establece otro criterio (ya se estableció uno con la prueba de la primera derivada) para determinar los extremos relativos de una función en un número. A diferencia de la prueba de la primera derivada en la que se investigaba el signo de f ' a la izquierda y a la derecha de un posible extremo relativo, en la prueba de la segunda derivada solo se involucra al # crítico.
 |  |
 | |
Prueba de la primera derivada para la determinación de máximos y mínimos.
Criterio de la primera derivada
Se llama Criterio de la primera derivada al método o teorema utilizado frecuentemente en el cálculo matemático para determinar los mínimos y máximos relativos que pueden existir en una función mediante el uso de la primera derivada o derivada principal, donde se observa el cambio de signo, en un intervalo abierto señalado que contiene al punto crítico  .
.
 .
.
"Sea  un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue."
 un punto crítico de una función
un punto crítico de una función  que es continua en un intervalo abierto
que es continua en un intervalo abierto  que contiene a
que contiene a  . Si
. Si  es derivable en el intervalo, excepto posiblemente en
es derivable en el intervalo, excepto posiblemente en  , entonces
, entonces  puede clasificarse como sigue."
puede clasificarse como sigue."
1. Si  '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.
 '
' cambia de positiva a negativa en
cambia de positiva a negativa en  , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
.
2. Si  '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
 '
' cambia de negativa a positiva en
cambia de negativa a positiva en  , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
Suscribirse a:
Entradas (Atom)



